Okay, so say we get given information on the marks that a class got as a frequency table, like this:

Mean of grouped data

Normally to find the mean of some numbers, we just add up all the numbers and then divide by how many there are.  In this case though, we don’t have the individual numbers to add up.  Instead, we know how many numbers there are in each class, where a class covers a range of numbers like 1 – 5 for instance.

Although we don’t know what the exact marks are in each class, we can guess what the average mark in each class might be.  For instance, say we look at the “6 – 10” class.  Although marks in this class could be as low as 6, or as high as 10, the average mark is probably going to be around the midpoint, or “8”. 

So say we wanted to add up all the marks that belong to the class “6 – 10”.  One way to do this is to multiply the midpoint of that class by the number of exam scores that are in that class.  For “6 – 10”, the midpoint is “8”.  There are 5 marks exam scores in that class.  So the sum of all the marks in that class would be:

                                          

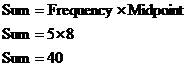
Now I just happen to have the original data here:

                   14, 7, 17, 15, 19, 13, 8, 9, 20, 3, 15, 17, 12, 6, 19, 15, 11, 10, 19, 14

The numbers in this list that belong to the “6 – 10” class are 7, 8, 9, 6, and 10.  What’s their sum?

                                                  

So the sum I get using the frequency table happens to be exactly right!  Let’s try doing this with the “16 – 20” class:

                                          

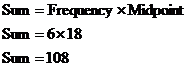
And using the original data, the numbers that fit into this class are:

                                                    17, 19, 20, 17, 19, 19

These add up to give:

                                           

For this class, the sum we get using the frequency table isn’t exactly right, but it’s pretty close.  In general, getting the sum of numbers in a class by multiplying the midpoint by the frequency is a good way of getting a pretty good answer.  Just remember it won’t be perfect!

Once you start doing this regularly, it makes it easier if you add another column to your frequency table.  We can call the frequency ‘f’ for short, and the midpoint ‘x’.  The column you want to add to your table is going to contain the product of the frequency and the midpoints, or ‘fx’ in mathematical terms.

Now remember what we’re trying to do here – we’re trying to find the average mark for this school class.  To do this we need to add up all the marks and divide by the number of marks.  To help us do this, it pays to add two boxes to our table, one below the frequency column, and one below the ‘fx’ column.  In these boxes we’ll put the sum of all the frequencies, and the sum of all the ‘fx’s:

If you haven’t seen it before, the symbol is called a ‘sigma’ symbol, and is an operation that means, “add up all the things to the right of it.”  In this case, it means to add up all the ‘fx’s, which are in the right column.

The sum of all the frequencies is often called ‘n’, sort of for “total (n)umber”.  In this case, n = 20.

So let’s find our mean.  We want to add up all the marks, which can be done by adding up the ‘fx’ column, and then divide by the total number of marks, which is n.  In mathematical form, this is:

                                                         

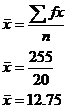
So the average mark for this class is 12.75.

Median of grouped data

This one’s a bit hard to work out exactly, but you can find out approximately what the median is though.  First of all, the median is the middle value.  We’ve got 20 exam scores all up, so we’re interested in the 10^th and 11^th scores.  Where are the 10^th and 11^th scores?  Well, what we can do is add a cumulative frequency column to our table, which shows the total frequency, adding in a downwards direction:

See how the cumulative frequency keeps track of how many exam scores in total you’ve gone through as you go down the table.  So by the time you’ve got through the 1^st ‘1 – 5’ class, you’ve only gone through one score in total.  But by the time you’ve gone through the whole “6 – 10” class, you’ve gone through 6 scores in total – 1 from the “1 – 5” class and 5 from the “6 – 10” class, making 6 in total.

Now we’re after the 10^th and 11^th scores!  Which class are these going to be in?  Well, according to our cumulative frequency column, the 10^th and the 11^th scores are going to be somewhere in the “11 – 15” class.  This is because before we go into this class, we’ve only counted 6 scores, but after we are through it, we’ve counted 14 scores.  The 10^th and 11^th scores must be somewhere in that class.

Now we can make a slightly better guess at what the median is.  We can look at where within the “11 – 15” class the 10^th and 11^th values are going to be.  Well, 10 and 11 are about halfway between ‘6’ and ‘14’, which are the number of scores before and after we go through this class.  This tells us that the median value is probably about halfway through this class.  So what’s halfway between 11 and 15?  About 13.  So we can say that the median mark is probably about 13.

Cumulative frequency graphs

You can also draw a graph using the cumulative frequency information and find out a median value that way.  On the x (horizontal) axis you need to put the marks, and on the y (vertical) axis you need to put your cumulative frequency.  The points you need to plot are the boundary points between classes – for instance one point would be for a mark value of 5 and a cumulative frequency value of 1.  The next point would be for a mark value of 10 and a cumulative frequency of 6.  Once you’ve done all the points, you just need to join them with straight lines:

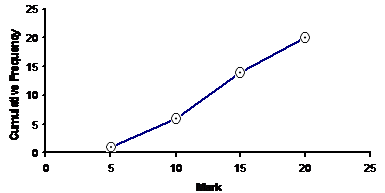
To find the median value, you’re looking for the middle value out of the whole lot.  We’ve got a total of 20 students in the class, so the median mark will be the average of the 10^th and 11^th students’ marks, when the marks are put in order.  In effect we’re looking for the mark the 10.5^th student got.  Our graph shows the students’ marks in order, starting from 5 and going all the way up to 20.  So what we can do is trace across from ‘10.5’ on the cumulative frequency axis until we hit our line, and then trace vertically downwards to the mark axis to find the median mark:

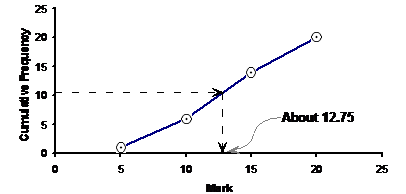
So from our graph, our median value is probably around 12.75, or about 13, which matches with what we got by looking at the table and intelligently guessing what the median value was.

What does having straight lines between points on the graph actually mean?  Well, it implies that the marks in each class (for instance in the 6 – 10 mark class) are evenly distributed within that class.  This is an assumption we make that is a reasonable one, although it’s not always going to perfectly correct.

Mode of grouped data

We don’t generally talk about a modal value when we’re dealing with frequency tables.  Instead, we talk about a modal class – the class which has the most values in it.  So all we do is look down the frequency column (not the cumulative frequency column), and find the largest number in it.  This corresponds to the modal class.

In this case the class with the most marks in it is “11 – 15” – it has 8 values in it.  So the modal class is the “11 – 15” class.

Sometimes of course you get two or more classes which both have an equal maximum number of values in them.  In this case you have to say that there are multiple modal classes, and then list them.  For instance, say we had a table like this:

You’d say there are two modal classes – “1 – 5” and “11 – 15”.