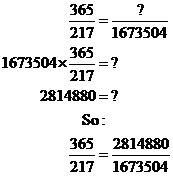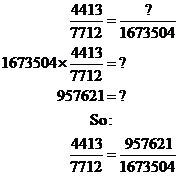Multiplying rational numbers together

When you multiply two rational numbers together, the answer you get is a rational number as well.  Why is this?  Well, when you multiply an integer by another integer, you get an integer.  Say I have two rational numbers multiplied together:

                                     Rational Number 1 × Rational Number 2

A rational number can be expressed as a fraction with an integer on the top and on the bottom:

                                

Now what happens when you multiply the tops and bottoms of these fractions?  Well, the top multiplication is an integer multiplied by an integer.  We know that this will give us another integer.  Same with the bottoms – multiplying together two integers will give us an integer as an answer.  So overall, our new number will be:

                                                

When is a number a rational number – when it can be written as a fraction with an integer on the top, and an integer on the bottom.  What do we have here – a rational number!  So multiplying together rational numbers gives you an answer which is itself a rational number.

Dividing rational numbers

When you divide one rational number by another, the answer you get is a rational number as well.  You can show why this is in almost exactly the same way as in the previous section.  The only extra thing you’ll need to remember is that:

                                             

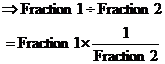
Adding and subtracting rational numbers

When you add or subtract rational numbers, the answer you get is always a rational number.  Why is this?  Well, take these two rational numbers and add them together:

                                                       

Before you can add them together, what do you have to do?  You need to find a common denominator.  One quick way of doing this is to multiply the two denominators together:

                                    

You can then change each fraction so that it has this new denominator:

Now you can add them together, because they have a common denominator:

                                               

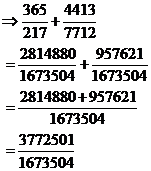
Is this answer a rational number?  Yes it is!  Why?  Because there’s an integer on the top of the fraction, and an integer on the bottom.  When you add together two rational numbers, you will always be able to find a common denominator for the two fractions.  This means you’ll always be able to add them together, and your answer will always have an integer on the top and an integer on the bottom, making it a rational number.  Sometimes the integers will be large and complicated, like in this case, but that doesn’t matter.  They’re integers, so the number is rational.  End of story.

Using a dot instead of a multiplication symbol

Say a question asks you to find the factors of a number, perhaps the number 20.  After trying various numbers you should be able to work out that its factors are 2, 2, and 5.  How can you show that these are the factors of 20?  Well, one way you can is by showing that you can get 20 by multiplying them together, like this:

                                                       

Sometimes, when you’re showing the factors of a number, people use a dot instead of the multiplication symbol, like this:

                                                         

Now obviously this might be a little confusing, because the dot looks just like a decimal point.  There are a few ways to stop getting them mixed up however.  There is usually only one decimal point in a number.  In this example, there are two dots, so this tells us they’re probably not decimal points.  Also, these dots are usually only used to show factors of a number, so if you’re not in a question dealing with factors the dot is probably a decimal point.  The last thing you can do is to see whether the dot makes sense as a decimal point.  For instance, say I had something like this:

                                                           

Does ten really equal two and a half?  No it doesn’t!  So the dot isn’t a decimal point.  Perhaps the dot is acting as a multiplier?  Let’s see if that makes sense – you can do this by replacing the dot with a multiplication symbol and seeing if it makes sense:

                                                          

Ten does equal ten, so the dot is acting as a multiplier.  This expression is showing us the factors of ten, and how they multiply together to give ten.

Working with the number zero

The number zero is a unique number which has all sorts of special properties:

Any thing you multiply by zero will give you an answer of zero.  For example:

                                           

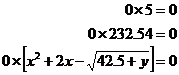
Adding zero to anything, or subtracting zero from anything won’t make any difference to that thing – it will be unchanged.  For example:

                            

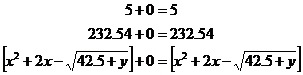
The tricky part of working with zero is when you try and divide something by zero.  Dividing by other numbers is easy, for instance if I divide 6 by 2, I know the answer is 3.  There are ‘3’ lots of ‘2’ in the number 6.  What about if I have this division:

                                                             

This division is asking us, “How many zeroes are there in one?”  Are there ten?  Well, ten lots of zero is still zero, which doesn’t make up one.  Perhaps there are one hundred?  Well, one hundred lots of zero is still zero, which doesn’t make up one.  What about one thousand?  One million?

You can keep on going until you get bored (you’re probably bored already).  So you can fit an unlimited quantity of zeroes into the number 1.  This makes it tempting for people to say something like, “There are infinity zeroes in one,” or, “There are infinite zeroes in one,” but this is wrong.  Infinity isn’t really a number.  When you divide a number by zero, you’re asking, “how many zeroes can I fit in that number.”  From what we’ve just done, we know that there isn’t any specific number of zeroes that fit into 1, or 3 or 10 or whatever.  So what we do is say that the answer to this problem is undefined.  This means that there is no answer that makes sense.