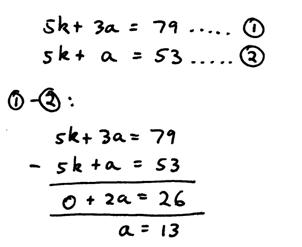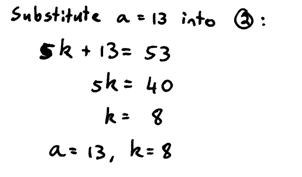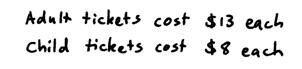When you solve for the unknowns in a simultaneous equation, what exactly are you doing? You’re given pieces of information – the equations, and unknowns – the ‘x’s and ‘y’s in the equations. But there is a graphical way of thinking about what you’re doing as well. What happens if you plot the simultaneous equations? Let’s do this with the last question, the two equations are:
Sponsored Links
So first of all, we need a pair of axes, one axis measuring ‘a’, and one measuring ‘b’:
Let’s plot our first equation. Because all the variables (‘a’ and ‘b’) are raised to the power 1, it’s a linear equation, which means it will come out as a straight line. This means we can plot the graph by just finding where the line will cross the two axes, and then drawing a straight line through those two points.
To find out where it crosses the ‘b’ axis, we just need to set ‘a’ to equal 0:
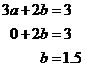
To find out where it crosses the ‘a’ axis, we just need to set ‘b’ to equal 0:
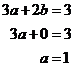
Now we just plot these two points, and draw a straight line through them:
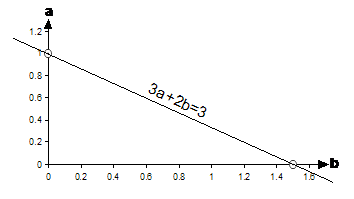
Same thing needs to be done for the other equation –
. The
‘b’ axis intercept is when ‘a’ = 0:
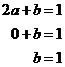
The ‘a’ axis intercept is when ‘b’ = 0:
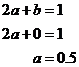
Put this on the graph as well and you get this:
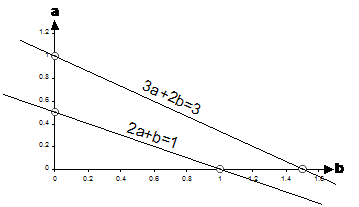
Now, when you find out the values of the unknowns
in the simultaneous equations, what you are doing is finding values of the
unknowns which make both equations true. If all we have to worry about is
, there
are lots of possible combinations of ‘a’ and ‘b that will make this true. Same
applies if all we have to worry about is – there are lots of combinations of
‘a’ and ‘b’ that will make this equation true as well.
If you think about this in terms of the graph – any
point along the straight line is a pair of (a, b)
values that make that equation true. Any point along the straight line is a pair
of (a, b) values that make that equation true. So where can I find a
pair of (a, b) values that make both equations true? The answer is –
where the two lines cross over. To find this point on our current graph, we’re
going to have to extend the b-axis a little:
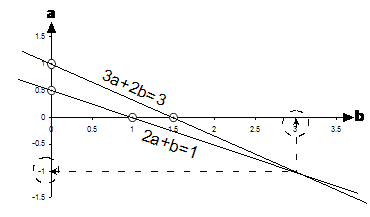
The two lines intersect at the point where b = 3 and a = –1. Do these numbers look familiar? They should. They were the values of the unknowns we calculated when we solved the simultaneous equations earlier.
If you plot the lines of two simultaneous equations, the coordinates of the point where they intersect are the solutions to the unknowns in the equations.
Choosing whether to graph simultaneous equations
Now you have two ways of solving simultaneous equations. You can find out the values of the unknowns by using the substitution method or elimination method. Or you can plot the two lines on a graph and find the solution by looking at where the two lines intersect.
Which method should you use? Well, whenever you plot a graph, you can’t draw it perfectly. Also, when you look at the intersection point of the two lines, you won’t be able to work out exactly where that point is. You’ll have a pretty good idea, but you won’t know exactly where it is. The point I’m making is that your answers using the graph method will be good but they won’t necessarily be exactly right. It’s especially hard to find the precise location of the intersection point when the lines are almost parallel:
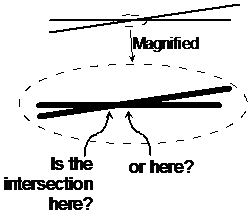
When you use the substitution or elimination method, if you don’t make any mistakes, your final answers will be exact. This means that if you need to get exactly the right answer, you’re better off not using the graph method.
Sometimes questions will specifically ask you to draw a graph – in which case, go ahead – draw a graph. Just remember that your answer will be close but won’t necessarily be spot on.
Simultaneous equations that produce parallel lines
Now you should be capable of plotting the straight lines for any two simultaneous equations and finding where they intersect. There is only one type of situation where you won’t be able to do this. You should always be able to plot the lines, but sometimes the lines won’t intersect. When will this happen? It will happen when the lines are exactly parallel to each other.
For instance, say we had these two simultaneous equations:
The graph of these two equations looks like this:
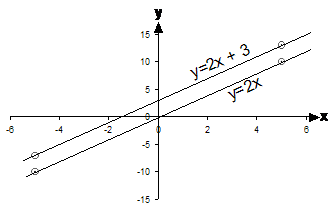
These two lines are perfectly parallel, which means that they’re never going to intersect. What does this mean? Well, normally, the coordinates of the intersection point are the solutions to the unknowns in the equations. If there’s no intersection point, what does this imply? That there are no solutions!
This becomes obvious if you think about the two simultaneous equations. There are no possible values of x and y that could make both equations true at the same time. Another way we can show there are no solutions is by using the substitution method.
Our second equation is:
Our first equation tells us that ‘y’ is equal to ‘2x’. So let’s substitute in ‘2x’ for y like this:
But 
, so:
This look strange, let’s simplify it anyway by cancelling out the ‘2x’ terms on both sides:
How can zero equal three? Well, quite simply, it can’t! Since we get equations that don’t make sense, this tells us that there are no solutions for the unknowns in these two simultaneous equations.
|
Going to the cinema 5 kids and 3 adults went to the cinema to see a movie. To save time, one of the kids bought all the tickets for everyone, which cost $79. The movie was so good though that after it finished, the kids all wanted to see it again. The adults were sick of it already, but one had to stay with the kids to supervise, while the other two went home. One of the kids bought all the tickets again, and it cost $53. Later, when everyone got home, they were trying to work out how much everyone owed. It was a little hard because they didn’t know the prices of adult tickets and child tickets. What were the prices? |
|
Solution |
|
Okay, there are a lot of words in the question, let’s try and break it into simple bits of information. There’s a group of kids and adults going to the cinema. The first time they see the movie, all 5 kids and 3 adults see it. It costs $79 for their tickets. We can write an equation showing this information in mathematical form: Let ‘k’ = price of a ticket for a kid Let ‘a’ = price of a ticket for an adult Then: So we’ve got one equation written down. How many unknowns are there – two – ‘k’ and ‘a’. But we’ve only got one piece of information so far – this equation. To work out what the unknown values are we need at least as many different pieces of information as there are unknowns. We can get another piece of information from later in the question. Turns out that the 5 kids and 1 adult see the movie again, and this time it costs $53. So we can write another equation: Fantastic – now we’ve got two unknowns – ‘k’ and ‘a’, but we also have two different pieces of information – the two equations. Now it just becomes a normal simultaneous equations problem: Which method should we use – substitution or elimination? To use the substitution method, we need to get one of the equations into the form “k = …” or “a = …” None of them are in this form currently, so we’d have to do a bit of manipulation of the equations. However, the elimination method would be easy to use – we already have two identical terms in the two equations – there is a ‘5k’ in both of them. So first we need to number the equations, and subtract one from the other:
This allows us to find the value of the unknown ‘a’ – it’s 13. So once we have this, we can use this value in one of our original equations to find the other unknown ‘k’:
Then we can summarise the values for our unknowns. Adult tickets are 13 what? Cents? Dollars? Well, we wrote our equations assuming ‘a’ and ‘k’ were measured in dollars, so it is good to write the units in at the end, something like this perhaps:
|
