There are two main methods that you can use to solve simultaneous equations.  One is called the substitution method, and the other is called the elimination method.  Each one has its own way of manipulating the equations so that you get a value for all the unknowns.  Usually the best thing to do is try both methods yourself, and then decide which one you like the best. 

The substitution method

The name should tell you what this method is all about. We’ll use a typical simultaneous equation problem with two equations to explain this method:

                                                       

To use this method, just pick one of the equations.  For this example, how about we choose the top one, .  Now, we’ve got two unknowns in this equation, ‘x’ and ‘y’.  What we want to do is pick one of these, and substitute something else for it.  So say we pick ‘x’.  We want to replace the ‘x’ with what it is equal to.

So what is ‘x’ equal to?  Well, this is where our second equation comes into play.  We can rearrange our second equation, so that it is in the form of “x = …”:

                                              

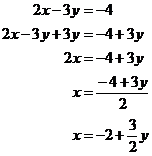
So now we have an expression that says what x is equal to.  We can substitute this into our first equation:

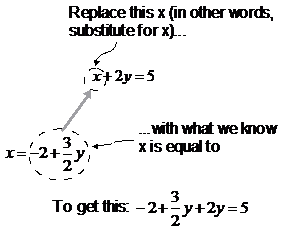
Now we’ve only got one unknown in this equation, so we can solve for the value of y:

                                                  

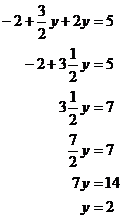
So we now know one of the unknown values.  It’s easy to solve what x is equal to – we’ve already got an equation in the form, “x = …” All we need to do is plug the value of y into it:

                                                      

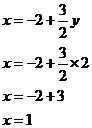
And now we know the values of both of our unknowns.  The method gets its name from the step where we substituted what x is equal to into the first equation.

Picking the right equation to substitute into

In this last example, the two equations were both about the same level of complicatedness.  Sometimes you’ll get a pair of equations like this though:

                                                       

The first equation is more complicated than the second equation.  The second equation is already nicely arranged in an “x = …” format.  Since it’s already like this, we can save time by using it to substitute directly into the first equation.  So in the equation , we can substitute ‘2y’ instead of ‘x’. 

Say we had gone the other way, and tried to substitute for ‘x’ in the second equation.  We’d have to rearrange the first equation into the form “x = ...”, before we could do the substitution.  This would take longer which is always a bad thing, especially in an exam.  So keep your wits about you when you choose how you’re going to do your substitution.

The elimination method

The elimination method is all about getting rid of one of the unknowns in the equations, by adding or subtracting the equations.  This is a new type of operation you might not have done before.  We’re all used to adding say 3 + 4 = 7, but what if you have to add two equations?  Well, this is how you do it:

If  is one equation, and  is another equation, I can add them by adding up like terms.  Like terms have the same letter symbols in them, raised to the same power.  So the ‘3x’ and the ‘2x’ are like terms.  The ‘4y’ and the ‘–2y’ are like terms.  And the ‘7’ and ‘4’ are like terms too.

Now, as I said before, the elimination method works by getting rid of one of the unknowns when you do this addition or subtraction with the two equations.  For the addition we just did, we ended up with another equation which still had two unknowns in it, so we missed something.  

To get rid of one of the unknowns, you need to change one of the equations so that it has exactly the same unknown term in it as the other.  To change the equation, you may have to divide it by something or multiply it by something.  Take these two equations for instance:

                                                        

Compare the ‘a’ terms – are they exactly the same?  No they’re not – one is ‘3a’ but the other is ‘2a’.  What about the ‘b’ terms – are they the same?  No they’re not – one is ‘2b’ but the other is just ‘b’.  So how could we change one of the equations so that it has exactly the same unknown term as the other?

Well, if we multiplied the second equation by 2, we’d end up with a ‘2b’ in that, just like in the first equation.  So let’s do that:

We can write down the 1^st equation and the new 2^nd equation again:

                                                        

Now that we have a ‘2b’ term in both equations, we can get rid of these terms by subtracting one equation from the other (doesn’t matter which one from which):

If –a is equal to 1, this must mean a = –1.  

Then, to work out what ‘b’ is equal to, you just need to substitute this value of ‘a’ into one of the equations, whichever looks nicest.  I’m going to pick the first equation:

                                                      

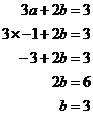
And now you have solved for the values of ‘a’ and ‘b’.

Adding equations using the elimination method

Sometimes with the elimination method you need to look for terms in both equations that are identical but which have the opposite sign – one is positive, one is negative.  In this case, you need to add the two equations to get rid of the unknown value.  For instance, if you had these two equations:

                                                        

By adding these two equations together, I could get rid of the ‘2b’ and ‘–2b’ terms:

Numbering equations

In order to get good marks on an exam or assignment, you want to make your solutions as easy as possible for the marker to read and understand.  Even if your answer is wrong, if it’s clearly set out there are several bonuses:

·         Your marker will be in a friendlier mood if it’s easy to read through your solution.

·         They will be able to clearly pick out where you’ve gone wrong, and you may get partial marks for your working anyway.

·         They will be able to tell you exactly where you went wrong so you can avoid making the same mistake again.

·         So if I was to write out a solution to the previous question in an exam, I might write it something like this:

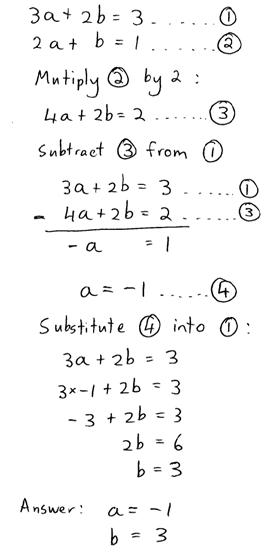
Notice how I’ve numbered the initial two equations 1 and 2, and how I’ve also numbered other important equations along the way.  This means whenever you do an operation, you can use these numbers in your description of what you’re doing.  Also at the end I’ve given a brief summary of the values of both unknowns.  It’s a good idea to do this even though you’ve already written the ‘a = –1’ part earlier in the solution.  It means once the marker’s read to the end of your solution, they don’t have to go back through it to find all your answers.