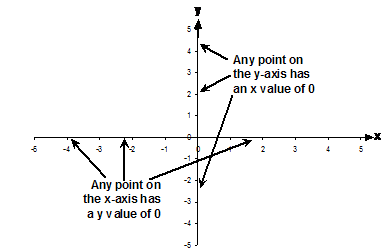
Intercepts are where the line crosses the x-axis and the y-axis.  Where the line crosses the y-axis is called the y-axis intercept.  At the point where the line crosses the y-axis, the value of x has to be 0.  This gives us a clue to finding what the y-axis intercept is – all we need to do is set the value of x to zero in the relation.

So our relation from before is .  What we need to do is set the value of x to zero, and then see what y is equal to.  This value of y is the y-axis intercept, the point where the line crosses the y-axis:

                                                       

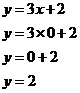
Now on to finding the x-axis intercept.  This is where the line crosses the x-axis.  Now, all along the x-axis the value of y is zero.  So what we need to do is set y to zero in the relation, and then work out what x is.  The value of x we calculate will be the location along the x-axis where the line intercepts it:

                                                    

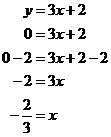
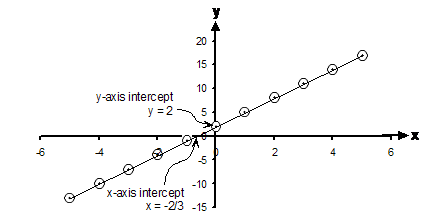
So we’ve found that this line has a positive gradient, an x-axis intercept at  and a y-axis intercept at 2.  Although we didn’t have to draw a graph to find out this information, here’s one anyway, with the intercepts shown on it.

So this is how you work out the intercepts of a straight line graph.  One thing you need to remember is that vertical or horizontal lines will only have one intercept.  For instance, the following relation:

                                                             

is a horizontal line, which means that it only intersects the y-axis.  Where does it intersect?  Well that’s pretty easy, we don’t even have to do any maths, we just need to look at the relation – it intersects the y-axis at y = 3!  Easy.