For once, a topic in mathematics which has an easy to understand name! Straight line graphs are just what they say they are – graphs which have a straight line in them.
Now you can get all sorts of straight line graphs – a line can be located anywhere on the graph and point in any direction. There are some mathematical terms which we can use to describe different types of straight line graphs, depending on what the line looks like. Here they are:
Sponsored Links
Gradient
Gradient means pretty much the same as the word slope. If you’ve ever been in a car driving up a steep hill, you may have seen a warning sign at the side of the road which looked something like this:

Now for most people in cars steep hills aren’t a worry, but if you’re in a heavy truck, sometimes you may have to take a detour because you don’t have enough power to get up the slope. So what exactly does a ‘1 in 4’ gradient mean? Well, this basically translates to “for every 4 metres you move in the horizontal direction, you move vertically 1 metre”.
Reading a gradient in the correct direction

Is this a slope upwards or downwards? Well, it can be either. If you look at it from left to right, it’s an upwards slope. But if you look at it going from right to left, then it’s a downwards slope.
Luckily, the general convention is that you read from left to right. So this picture would be considered an upwards slope.
Gradient types
Depending on whether a gradient is uphill or downhill there are two different ways to describe it. I’ll stop using the car example and start using graphs to show the meanings of these terms.
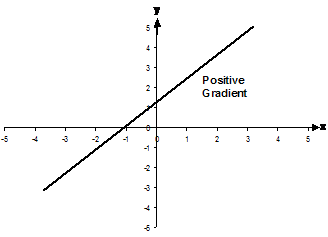
A positive gradient is when the slope increases as you move from left to right.
Here’s a positive gradient:
And a negative gradient:
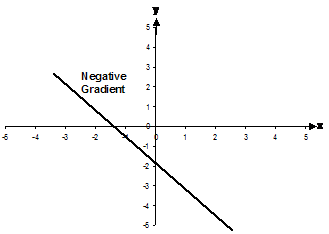
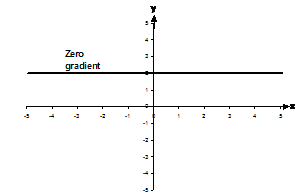
Horizontal lines don’t have a positive or negative gradient. Because they’re flat, we say that they have no gradient, or a zero gradient.
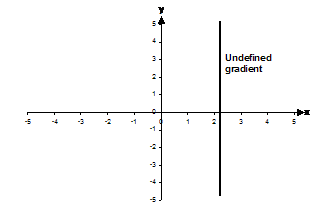
Vertical lines also don’t have a positive or negative gradient. Because they’re straight up and down, we usually say that they have an undefined gradient.