Mathematically there is a way to specify a relation, which you may get in a question. It looks something like this:
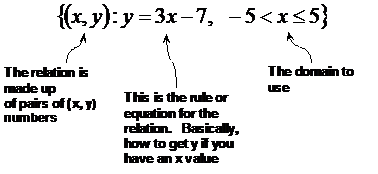
Sponsored Links
So for this relation, the domain contains all the values greater than negative five, up to and including positive five. Be careful here – note how one of the signs is just a smaller than sign, but the other one is a smaller than OR equal to sign. So a nice set of numbers which would represent this domain would be –4, –3, –2, –1, 0, 1, 2, 3, 4, and 5.
If the question asked you to plot the graph for this relation, first you’d choose your domain values using the instructions at the end of the expression. Then you’d use the middle part of the expression, the rule, to work out all the range values. Then you’d just need to choose a suitable layout for the x-axis and y-axis and then draw the points on.
Working out the range and domain from a graph
Sometimes you get asked what the range and domain of a graph is. Say you got given this graph:
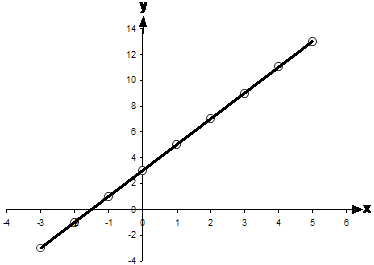
What you need to do is work out the smallest and largest ‘x’ values that this line has – that will give you the domain. Then you need to work out the smallest and largest ‘y’ values that this line has – that will give you the range.
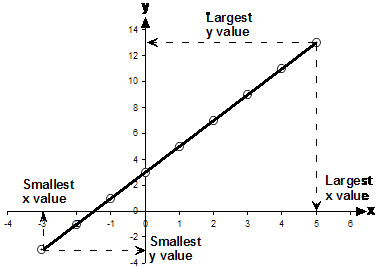
In this graph the smallest x value is –3 and the largest x value is 5. The x values are to do with the domain, so the domain contains numbers from –3 up to and including 5. So in mathematical format, the domain is:
![]()
Make sure you use the smaller than or equal symbols. If we just used smaller than symbols, then we would be saying that –3 and 5 weren’t part of the domain.
Next up is the range – we need to look at the y values for this. The smallest y value is –3, and the largest is 13. So the range can be written like this:
![]()
Domain and range for horizontal and vertical lines
Normally the domain and range contain a spread of numbers, for instance perhaps from –5 to +5. Sometimes however the domain or range can contain just one number. When you have a vertical line, there is no spread of x values – the entire line has the same x value. There are still a number of different y values though.
The opposite goes for a horizontal line – which has the same y value for all points along the line. There are still a number of different x values along the line though. So if you have to write down what the domain or range is for a vertical or horizontal line, one part is always easy.
Horizontal Line
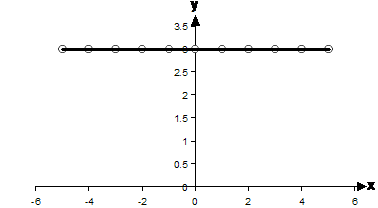
So for a horizontal line, the y values of all the points on the line are the same. For this particular relation, the y values are all equal to 3. Y values are to do with the range, so for this relation we can say that the range is:
![]()
Vertical Line
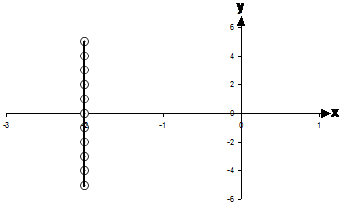
For a vertical line, the x value of all the points on the line is the same. For this particular line, all the points have an x value of ‘–2’. The x values are to do with the domain of a relation. So for the relation shown in this graph, we can write that the domain is:
![]()

