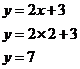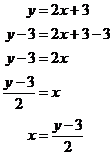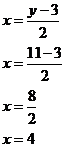Mathematical relations

Often in mathematics we come across equations or rules that you can use on numbers to get other numbers.  For instance, one rule could be, “take the number and double it.”  If I used the rule on some numbers, I’d get something like this:

See how I get all these pairs of numbers?  Each horizontal line in the table forms a pair.  You can write these pairs of numbers like this:

                                         (Number, number after using rule)

For our numbers the pairs are:

                                                               (2, 4)

                                                              (5, 10)

                                                             (–3, –6)

Since these pairs are all created using the same rule, we can group them together to form a relation like this, using curly brackets:

                                               { (2, 4), (5, 10), (–3, –6) }

Domain

The domain contains the set of numbers before we use the rule – they are the original numbers.  In our example, the domain contains the numbers 2, 5, and –3.  Usually the domain contains a continuous sequence of numbers, like 1, 2, 3, 4… for instance.  When you plot relations on a graph, the numbers in the domain are usually called the ‘x’ values, since they are plotted against the x-axis on a graph.

Range

The range of numbers is what you get after you apply the rule or equation to all the numbers in the domain.  In our example the range contains the numbers 4, 10, and –6.  When you plot relations on a graph, the numbers in the domain are usually called the ‘y’ values, since they are plotted against the y-axis on the graph.

Using tables to show a range and domain

Often in a question you’ll need to show the values in a mathematical relation in a table.  Usually you’ll get some values given to you in the table, and you’ll have to use these numbers to work out what should be in the empty boxes.  For instance, this question:

Table range and domain question

The relation is y = 2x + 3.  Fill in the table: x 2 4 8 5 –3   y           11

Solution

First of all, take note that now the table is in a different form – the top row of numbers are the domain – the numbers before we do anything to them. The bottom row of numbers is the range – the numbers after we apply the rule.  Tables can be in either form – horizontal like this one, or vertical like the first one in this section.  Either way, the range and domains are just lines of numbers next to each other, in one case they’re horizontal lines, in the other they’re vertical lines. To work out all the missing y values, we just need to use the rule y = 2x + 3.  So for the first column, when x = 2:                                                         We can do the same for all the other columns except for the last one.  In the last column, we’re given a y value, but not an x value.  We need to go backwards.  At the moment, our rule tells us what the value of y is if we know x.  We need to rearrange this equation so it gives us what x is if we know y:                                                     Now we just need to put in the value of y = 11 into this equation:                                                           So our final table should look like this: x 2 4 8 5 –3 4 y 7 11 19 13 –3 11 Notice how we’ve got two of the same pair – (4, 11) is in the table twice. Now showing relations in a table is all well and good, but it’s not that easy to ‘see’ the relationship.  To do that you need to plot the relationship in the Cartesian plane.  This is covered in the next section.