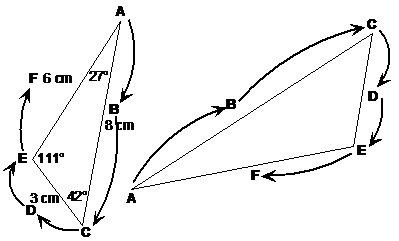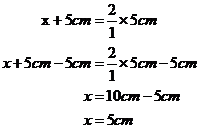Ratios are used a lot in geometry, especially when comparing shapes of different sizes and also lengths of the sides of shapes. In a lot of situations you can find equivalent ratios in a diagram, which can help you find how long a side of a shape is.
Proportional or similar shapes
Check out these two rectangles:
Sponsored Links

What is the ratio between the width and the height of the smaller rectangle? Well, it’s 2 cm wide and 4 cm high, so the width:height ratio is 2:4, which simplifies to 1:2. What about for the larger rectangle? It’s 4 cm wide and 8 cm high, so the width:height ratio is 4:8 which simplifies to 1:2.
Notice how both rectangles have the same width to height ratio. Mathematicians would describe these rectangles as being in proportion to one another. Or you could just say that the two rectangles are proportional. Another word which means the same as proportional is similar. So these two rectangles are also similar.
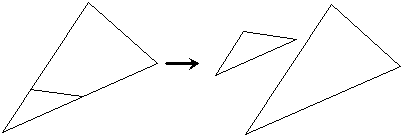
Similar shapes don’t have to be lined up nicely, which sometimes makes your job identifying them a bit harder. For instance, these two shapes are similar:

Because the small shape has been rotated quite a bit compared to the larger one, it’s hard to compare the two in your mind. One way to compare them in your mind is to mentally rotate the smaller shape until it’s at the same angle as the larger one, and then mentally place it inside the larger one like this:

Getting good at doing this rotation in your mind is important, because it can help you avoid getting tricked by situations like this:
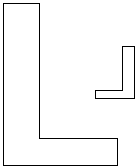
You might think that these two shapes are similar, since they both look like block letter ‘L’s. However, just in case, let’s rotate the smaller shape and try and align it inside the larger one:
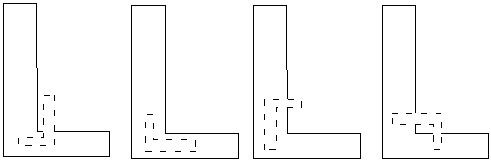
No matter what way we rotate the smaller shape, it never looks like a smaller version of the large one. The closest it gets is at the 2nd attempt, but even then the long part of the small ‘L’ is in the short part of the large ‘L’, and vice versa.
Similar or proportional shapes have the same shape, but are different sizes. There is however a word for shapes that are exactly the same:
Congruent shapes
If you have two identical shapes:

they are said to be congruent. Congruent shapes are the exact same size and the exact same shape. Because they have the exact same size and shape, this means that congruent shapes must have equal angles and equal side lengths as well.
How to tell if two shapes are congruent
There are a few tests you can use to decide whether two shapes are congruent.
Can you move or rotate one shape so that it covers the other shape exactly?

Is one shape the mirror image of the other?
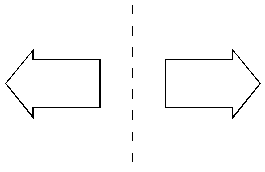
These are congruent shapes, since they are mirror images of each other. Remember that to be a mirror image, they must be the same size.
Are all corresponding sides lengths and angles the same?
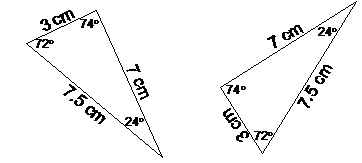
These two triangles are congruent, since all corresponding angles and side lengths are the same. Corresponding means you have to compare the same bits in each triangle, for instance the shortest side in one triangle corresponds to the shortest side in the other triangle.
You can also use some general knowledge and reasoning to help you work out whether two shapes are congruent. For instance, with triangle shapes, there are 4 things you can look for to tell whether two triangles are congruent:
Congruent triangles
Two sides are equal in length, and the angles included by these sides (in between them) are equal.

This is known as SAS – (S)ide (A)ngle (S)ide.
A pair of angles on one triangle is equal to a pair of angles on the other triangle, and the side between these angles in one triangle is equal in length to the corresponding side in the other triangle.

This is known as ASA - (A)ngle (S)ide (A)ngle.
Three sides on one triangle equal in length to corresponding three sides on the other triangle.

This is known as SSS – (S)ide (S)ide(S)ide.
For right-angled triangles you don’t need as much information as to whether they are congruent or not. All you need is two corresponding sides to be the same length:
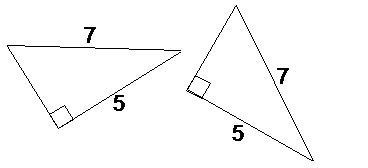
|
A lot of proportional and similar shape type questions use triangles. For instance, you might get two shapes like these ones and be told that they are similar shapes. The question would then ask you to write in all the information on the second shape. Here’s one: These two shapes are similar. The side lengths of the larger, unlabelled shape are all 1.5 times larger than for the smaller, labelled shape. Label the larger shape with all three side lengths and all three angles.
|
|
Solution |
|
One way to do these questions is to pick a point on one shape, and work out which point it corresponds to on the other shape. In this case, because it’s an easy point to pick out, we’ll pick the top corner on the smaller shape, which I’ve marked ‘A’. Now, which corner on the new shape does this corner correspond to? Well, we’re looking for the corner at the narrowest part of the triangle, which is the bottom left corner on the new shape. What we can do now is starting at this corner on both shapes, move in a direction towards the longer side touching that corner and keep going. In this case this means a clockwise direction for both shapes. As we go around we add information. Every time we get to either an angle, or the length of a side, we need to transfer information from the labelled shape to the unlabelled shape.
This diagram shows me starting at point A on both diagrams, and moving in a clockwise direction around both shapes. Every time I’ve got to an angle or a side length, I’ve given it a letter as a label, to show which parts of each shape correspond to each other. Now all I have to do is on the second shape, instead of writing the letters, write down the value next to the letters in the first shape. The question mentioned that the side lengths in the larger shape are all 1.5 times larger than in the smaller one. We need to take this into account when we label the side lengths on the larger shape. We need to make them all 1.5 times larger. So for ‘B’, instead of writing 8 cm, we need to write 12 cm. At ‘D’, instead of writing 3 cm we need to write 4.5 cm. At ‘F’ we need to write 9 cm instead of 6 cm. So instead of A, I write down 27° since this is the angle at A. Instead of B, I write down 12 cm, since this is 1.5 times the length at B in the smaller shape. Instead of C, I write down 42°, since this is the angle at C. And so on…eventually you should have a diagram like this:
If one of the two similar shapes has been flipped, you may end up going in a clockwise direction on one shape, but an anti-clockwise direction on the other, using the rule of heading towards the longer side touching your starting point. |
Similar triangles inside triangles
This is one common type of arrangement of triangles which allows you to exploit your knowledge of similar triangles. I’ll show how to do this through another question:
|
Find x and y:
|
|
Solution |
|
You should be able to see two triangles in this diagram. The outside border forms a large triangle, and there is also another smaller triangle in the left half of the diagram. Now, this by itself doesn’t mean that these are similar triangles. For instance, say we had something like:
You would know that these aren’t similar triangles because they aren’t they same shape. If you draw them separately it is pretty easy to see this. However, in our case, we have some extra information. Our two triangles have their right side at the same angle, 78°. When you split them up, because their right sides are at the same angle and share the same bottom side, you can see that they are similar triangles:
We have to work out what the values of ‘x’ and ‘y’ are in the diagram. We can do this by our knowledge of corresponding sides in the similar triangles. For instance, the side with ‘y’ on it in the smaller triangle corresponds to the 7 cm side of the larger triangle. Since they are similar triangles, we know that the ratio between the side lengths in the smaller and larger triangles is the same, for all the sides. So what we need to find is a side which we have a length for in both the small and large triangles. Once we get this information, we can work out the ratio between the two side lengths.
We have information for both the bottom
sides of the two triangles. The small triangle’s bottom side is 5 cm long.
The large triangle’s bottom side is In fraction form: This tells us that sides in the big triangle are twice as long as sides in the small triangle. That’s all we need to work out x and y. Let’s do y first. It corresponds to the 7 cm long side in the big triangle. We know that sides in the small triangle are half as long, so we need to divide 7 cm by 2, which gives us 3.5 cm. So y = 3.5 cm. Next we need to work out what x is. We have to be a bit more careful here – notice that x does not measure the whole length of a side on the big triangle. The whole length of the left side of the large triangle is actually x plus 5 cm.
So we can use our ratio to work out what x is: So at this stage, we can substitute in what we have for our large side length and small side length: |