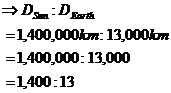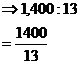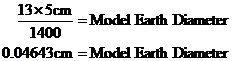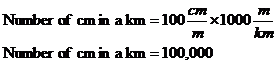Sometimes you have to change units before you can write down a ratio. For instance, say you had to write the ratio between 50 metres and 2 kilometres. Metres and kilometres are different units, but they measure the same type of dimension – they both measure length. So to write a ratio, I’d need to convert one of the amounts into the same units as the other. Usually, it’s better to convert the bigger units of measure into the smaller units of measure. This way can help you avoid decimal numbers in your ratios.
In this case, the bigger unit of measure is a kilometre, so we’ll convert the amount measured in kilometres into metres. We know there are 1000 metres in a kilometre, so to convert we do:
Sponsored Links
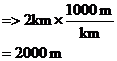
Now we can write the ratio between the two distances:
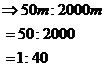
|
Using ratios to create models of the Earth and the Sun question |
||||||||||||
|
The Earth and the Sun are two very huge objects which are very far apart. Sometimes people create models of the Earth and the Sun to help give people an idea of their relative sizes and also how far away they are from each other. Here’s some information on the sizes of and distances between the Sun and Earth in real life:
In our model, we are going to use an orange which has a diameter of 5 cm to represent the Sun. How big should our model Earth be, and how far from our model Sun should we put it? |
||||||||||||
|
Solution |
||||||||||||
|
So first, we can summarise what we know about the real world and our model like this:
Part 1 – Working out the size of our model Earth Now, in the real world the Earth is quite a bit smaller than the Sun. How much smaller? Well, we can write a ratio between their two sizes like this: So we have a ratio between the size of the Sun and the size of the Earth. We can use this to work out how big our model Earth should be. First, we can rewrite this ratio as a fraction: This ratio is the ratio of the Sun and Earth’s sizes in the real world. But the model should have the same ratio between the sizes of the Sun and Earth. So we can write down: We want to work out the diameter of our model Earth, so we need to rearrange the equation so it’s the only thing on one side. First we can swap tops and bottoms: Then we multiply both sides by “Model Sun Diameter”: Now we know how big the model Sun is – 5 cm, so we can write it in, and calculate the model Earth’s diameter: So our model Earth only has to be a fraction of a centimetre in diameter. Next we have to work out how far apart the model Sun and Earth should be. Part 2 – Working out how far apart the model Sun and Earth should be Obviously they’re going to be a lot less than 150 million kilometres apart in our model. But how much less? Well, how much the diameter of the Sun shrinks going from the real world to our model, is the same as how much the distance will shrink going from the real world to our model. The ratio of the Sun’s diameter between the real world and the model is: Whoops! We’ve got different units here. Let’s put everything into centimetres. How many centimetres in a kilometre? Well, there’s 100 centimetres in a metre, and 1000 metres in a kilometre. So: So to change 1,400,000 km to cm, we need to multiply it by 100,000. It becomes 140,000,000,000 cm!!! So our ratio between the Sun’s diameter in the real world and the model is: or in fraction form: So this tells us that measurements in the real world are 28 billion times larger than in our model. We know that the ratio between the Sun’s real size and model size is the same as the ratio between the real distance and the distance in our model. This mean we can write an equation equating these two ratios: We want to find out the model distance, so we want to get it all by itself. To do this we need to rearrange the equation, first by swapping tops and bottoms: And then by multiplying both sides by ‘Real Distance’: Now the fraction on the left hand side is the inverse of the ratio we just calculated. It is the ratio of the model Sun diameter to the real Sun diameter. We just calculated the ratio of the real Sun diameter to the model Sun diameter. See how they are the opposite of each other? Before, we calculated that: Now, we’ve got: It’s just the same fraction with tops and bottoms swapped over. So the numbers should swap too: Now we can put this into our overall equation: Once we do the calculations we get our answer – the model Sun and model Earth need to be placed 5.4 metres apart. |