Ratios

Say you’ve gone down to the shop to buy some electrical cable so you can put together a home entertainment system.  You need 5 metres of the stuff, but the price tag says something like, “$7.00 per 2 metres.”  How do you work out how much 5 metres is going to cost?

Well, you know it’s going to cost more than $7.00, because that’s how much 2 metres costs, and you need 5 metres!  One way you might do it is to work out how much 1 metre of cable costs, and multiply that by 5 to work out how much you need to spend:  

                                                                   

                                    

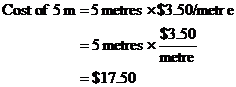
Now there’s another way you can work out how much 5 metres would cost, by using ratios.  Ratios tell you how many times bigger or smaller one thing is than another.  The things that a ratio compares have to have the same units.  In this example, we have two lengths (measured in metres), a ‘2 m’ length which is what the price is given for, and a ‘5 m’ length, which is how much we want to buy.  We can express these two lengths as a ratio, by taking one and dividing it by the other:

                                               

We can also form another ratio from the information in this question.  We have prices (measured in dollars).  One price is $7.00, which is how much the cable costs per 2 metres.  The other price is how much we are going to have to pay for 5 metres of cable, and is an unknown amount at this stage.  We can use an ‘x’ to represent this amount.  We can write this ratio like this:

                                              

So now we have two ratios, a ratio involving lengths of cable, and one for the prices.  Now, if we make sure the tops and bottoms of the two ratio fractions are corresponding, we can equate them (make them equal).

Looking at the tops of the ratio fractions, the 5 metres corresponds to how much cable we want to buy.  This corresponds to the amount we’re going to have to pay for 5 metres, which is ‘x’.  But ‘x’ is on the bottom of the other ratio fraction.  So we need to swap its top and bottom like this:

                                              

Now we can equate the two ratios:

Now we’re interested in how much we’re going to have to pay for 5 metres.  We’ve already given this amount a name – ‘x’.  So we just need to manipulate this equation until we get an “x = …” arrangement:

                                                       

Multiply both sides by $7.00:

                                                     

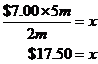
And we get the same answer as we got doing this problem the other way.

Ratios and colons

Ratios can also be expressed using colons, instead of using fractions.  Say I want to compare the weights of two people.  Person A weighs 100 kg, and person B weighs 50 kg.  If I want to compare their weights using a ratio, I can use a fraction:

                                            

Or I can use a colon.  To convert a fraction into a ratio with a colon in it, read from the top of the fraction downwards, and replace the horizontal line with a colon, like this:

                                                       

Since ratios compare things which have the same units, often you just leave the units out:

                                                           

You can also simplify it by dividing both sides by the same numbers.  In this case, I can divide both sides by 50 and get:

                                                              

If I wanted to say this out aloud, I’d say something like:

                “The ratio of person A’s weight to person B’s weight is two to one.”

Equivalent ratios

Equivalent ratios are just ratios that mean exactly the same thing.  In the previous example,  and  are equivalent ratios, because they mean exactly the same thing.   is just a simplified version of

Simplifying ratios with zeroes

If I have something like , I can quickly do a lot of simplification by just crossing out the same number of zeroes in both numbers.  So, by crossing out two ‘0’s in each number, I quickly get , which I can then further simplify by dividing both numbers by 4.  Then I get , which is the ratio in its simplest form.

Splitting things up according to a ratio

Say you’ve been doing some gardening on the weekend with a friend for a little bit of money.  At the end of the day, you’ve worked 7 hours, and your friend’s only worked 4 hours.  You get paid $110 for your efforts.  How should you split up the money between the two of you?

Well, you’re going to have to split up the money based on how many hours each of you worked.  Since you worked more hours, you’re going to get a larger chunk of the $110.  But how much will it be exactly?  First we can write a ratio of how many hours you worked, to how many hours your friend worked:

                                   

How many hours is that all up?  Well, 7 + 4 = 11 hours.  So all up, you together did 11 hours of work.  This is how we can split up the money.  You split the $110 up into 11 bits first.  Then, because you worked for 7 of these 11 bits, you get 7 times this amount.  Your friend worked for 4 of these 11 bits, so he/she gets only 4 times this amount.  Basically, each of these ‘bits’ corresponds to an hour of work by one person.  So first we split up the $110:

                                                     

Now this $10 represents one hours work by one person.  You did 7 hours work, so you should get 7 times this - $70.  Your friend gets 4 times this amount - $40.

This works for any situation – say I had to split up 48 kg of potatoes into a ratio 3:2:1.  All up there are 3 + 2 + 1 = 6 bits I need to split the 48 kg into.  48 kg split 6 ways gives me 8 kg – each bit is 8 kg.  The first part of the ratio is 3 – so 3 bits at 8 kg a bit = 24 kg.  The second part of the ratio is 2 – so 2 bits at 8 kg a bit is 16 kg.  The last part of the ratio is 1 – 1 bit is just 8 kg.  So the overall 48 kg gets split up into the following amounts:

                                                      24 kg, 16 kg, 8 kg

It’s always a good thing to check that it adds up to your total amount.  24 + 16 + 8 = 48 kg, so we’re all good.